Inex
The inex (plural inexes) is an eclipse cycle of 10,571.95 days (about 29 years minus 20 days). The cycle was first described in modern times by Crommelin in 1901, but was named by George van den Bergh who studied it in detail half a century later.[1] One inex after an eclipse of a particular saros series there will be an eclipse in the next saros series, unless the latter saros series has come to an end.
It corresponds to:
- 10,571.95 solar days
- 28.95 years
- 358 synodic months
- 388.50011 draconic months
- 30.50011 eclipse years (61 eclipse seasons)
- 383.67351 anomalistic months
- 386.94 sidereal months
- 8 eclipse sets
The 30.5 eclipse years means that if there is a solar eclipse (or lunar eclipse), then after one inex a New Moon (resp. Full Moon) will take place at the opposite node of the orbit of the Moon, and under these circumstances another eclipse can occur.
Unlike the saros, the inex is not close to an integer number of anomalistic months so successive eclipses are not very similar in their appearance and characteristics. From the remainder of 0.67351, being near 2⁄3, every third eclipse will have a similar position in the moon's elliptical orbit and apparent diameter, so the quality of the solar eclipse (total versus annular) will repeat in these groupings of 3 cycles (87 years minus 2 months), called triads.
Inex series last much longer than saros series. For example, inex series 30 started in saros series −245 in 9435 BC and will continue well beyond 15,000 AD. But inex series are not unbroken: at the beginning and end of a series, eclipses may fail to occur. However once settled down, inex series are very stable and run for many thousands of years. For example, series 30 has produced eclipses every 29 years since saros series −197 in 8045 BC, including most recently the solar eclipse of February 5, 2000.[2]
An inex also is close to an integer number of days (10,571.95) so solar eclipses on average take place at about the same geographical longitude at successive events, although variations of the moon's speed at different points of its orbit mask this relation. In addition sequential events occur at opposite geographical latitudes because the eclipses occur at opposite nodes. This is in contrast to the better known saros, which has a period of about 6,585+1⁄3 days, so successive solar eclipses tend to take place about 120° in longitude apart on the globe (although at the same node and hence at about the same geographical latitude).
The significance of the inex cycle is not in the prediction, but in the organization of eclipses: any eclipse cycle, and indeed the interval between any two eclipses, can be expressed as a combination of saros and inex intervals.
An example partial inex solar eclipse series
[edit]The following fourteen eclipses from part of inex series 52, which has been yielding eclipses every 29 years since saros series −115 in 5275 BC and will continue to do so beyond 15,000 AD.[3]
- Saros series 130: Solar eclipse of November 9, 1817
- Saros series 131: Solar eclipse of October 20, 1846
- Saros series 132: Solar eclipse of September 29, 1875
- Saros series 133: Solar eclipse of September 9, 1904
- Saros series 134: Solar eclipse of August 21, 1933
- Saros series 135: Solar eclipse of July 31, 1962
- Saros series 136: Solar eclipse of July 11, 1991
- Saros series 137: Solar eclipse of June 21, 2020
- Saros series 138: Solar eclipse of May 31, 2049
- Saros series 139: Solar eclipse of May 11, 2078
- Saros series 140: Solar eclipse of April 23, 2107
- Saros series 141: Solar eclipse of April 1, 2136
- Saros series 142: Solar eclipse of March 12, 2165
- Saros series 143: Solar eclipse of February 21, 2194
An example partial inex lunar eclipse series
[edit]These eclipses are part of Lunar Inex Series 40.
- Lunar Saros 123: Total Lunar Eclipse of 1826 Nov 14 (Micro Full Moon)
- Lunar Saros 124: Total Lunar Eclipse of 1855 Oct 25
- Lunar Saros 125: Total Lunar Eclipse of 1884 Oct 04
- Lunar Saros 126: Total Lunar Eclipse of 1913 Sep 15 (Micro Full Moon)
- Lunar Saros 127: Total Lunar Eclipse of 1942 Aug 26
- Lunar Saros 128: Total Lunar Eclipse of 1971 Aug 06
- Lunar Saros 129: Total Lunar Eclipse of 2000 Jul 16 (Micro Full Moon)
- Lunar Saros 130: Total Lunar Eclipse of 2029 Jun 26
- Lunar Saros 131: Total Lunar Eclipse of 2058 Jun 06
- Lunar Saros 132: Total Lunar Eclipse of 2087 May 17
- Lunar Saros 133: Total Lunar Eclipse of 2116 Apr 27
- Lunar Saros 134: Total Lunar Eclipse of 2145 Apr 07
- Lunar Saros 135: Total Lunar Eclipse of 2174 Mar 18
Solar Saros-Inex panorama
[edit]A saros-inex panorama has been produced by Luca Quaglia and John Tilley. It shows 61775 solar eclipses from −11000 (11001 BC) to +15000.[4]
Each column of the graph is a complete Saros series which progresses smoothly from partial eclipses into total or annular eclipses and back into partials. Each graph row represents an inex series.
The lifetime of each inex series is not simple due to long-term period variations in the synodic and draconic month lengths. One can see from the data file that in the future (around saros series 300) the graph is horizontal (meaning that after an interval of an inex the moon will be at the same latitude), whereas at the beginning of the panorama around 11,000 BC for the moon to come back to the same latitude at another eclipse required about one saros for every ten inex. This implies that back then 3580+223 or 3803 synodic months equaled 3885+242 or 4127 draconic months. So a synodic month was about 1.0851959 draconic months, as compared to about 1.0851958 today. This decrease by about 0.1 ppm can be compared to the decrease in the length of a tropical year by about 1 ppm in the last 10,000 years (see Tropical year). (Note that if the length of a sidereal month were constant, then a decrease in the length of a year would cause an increase in the length of a synodic month.) One source states that the draconic month is increasing by about 0.4 seconds (ca 0.16 ppm) per millennium whereas the synodic month is increasing by about 0.2 seconds (ca 0.08 ppm) per millennium, but doesn't explain why the draconic month is increasing faster.[5]
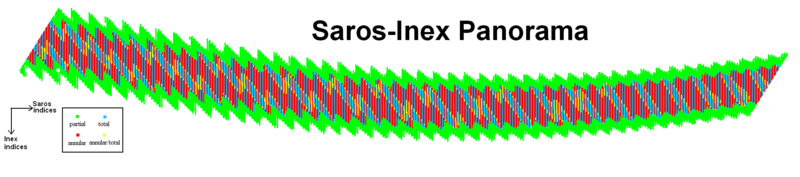
|
From the data file we can see that eclipses recur with a period of a combination of 15 inex and 1 saros (5593 synodic months, 165164.58 days, or 452.2 tropical years) throughout the whole panorama (26,000 years), for example from the eclipse of saros series −290, inex series 2 (slightly off the panorama to the left) to the eclipse of saros series 580, inex series 60 on the right-side edge of the panorama. Similar cycles with more or less than 15 inex per saros also cover the whole panorama.
Lunar Saros-Inex panorama
[edit]Lunar eclipses can also be plotted in a similar diagram, this diagram covering 1000 AD to 2500 AD. The yellow diagonal band represents all the eclipses from 1900 to 2100. This graph immediately illuminates that this 1900–2100 period contains an above average number of total lunar eclipses compared to other adjacent centuries.
See also
[edit]- June 2058 lunar eclipse § Inex_series, an example
References
[edit]- Andrew Claude de la Cherois Crommelin (1901), "The 29-Year Eclipse-Cycle", The Observatory, 24 (1901), 379–382 online link.
- George van den Bergh (1951), Regelmaat en wisseling bij zonsverduisteringen; met een aanhangsel over maansverduisteringen, 2 vols. H.D. Tjeenk Willink en Zoon N.V., Haarlem 1951.
- George van den Bergh (1954), Eclipses in the Second Millennium B.C. (–1600 to –1207): And how to Compute them in a Few Minutes H.D. Tjeenk Willink en Zoon N.V., Haarlem 1954.
- George van den Bergh (1955), Periodicity and Variation of Solar (and Lunar) Eclipses, 2 vols. H.D. Tjeenk Willink en Zoon N.V., Haarlem 1955.
- Jean Meeus (1997), Mathematical Astronomy Morsels Willmann-Bell, Inc., Richmond 1997 (Chapter 9 [pp. 49–55], "Solar eclipses: some periodicities").
Notes
[edit]- ^ George van den Bergh, Regelmaat en wisseling bij zonsverduisteringen; met een aanhangsel over maansverduisteringen (Haarlem: H.D. Tjeenk Willink en Zoon N.V., 1951), p. 20; George van den Bergh, Periodicity and Variation of Solar (and Lunar) Eclipses (Haarlem: Tjeenk Willink en Zoon N.V., 1955), p. 16.
- ^ Row 92 in Solar eclipse panaorama.xls. See Saros, Inex and Eclipse cycles for how to calculate dates.
- ^ See row 114 in Solar eclipse panaorama.xls.
- ^ Saros-Inex Panorama. Data in Solar eclipse panaorama.xls.
- ^ Fred Espenak (2012). "Periodicity of Solar Eclipses". NASA Eclipse Web Site. NASA. Archived from the original on 2016-07-22.

